Recall that one property of a rectangle is that opposite sides are always equal.
Therefore, we can say that:
DC = AB
BC = AD
Because of this, we can also say that DB = AC.
Given:
DC = 16.4 ft.
BC = 14.8 ft.
Using the Pythagorean Theorem, let's find DB.
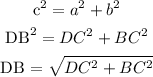
![\text{ DB = }\sqrt[]{16.4^2+14.8^2}\text{ = }\sqrt[]{268.96\text{ + 219.04}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/a51tdf0blff33pqmokaia6aqx8yvk9v51e.png)
![\text{ DB = }\sqrt[]{488}\text{ }\approx\text{ 22.1 ft.}](https://img.qammunity.org/2023/formulas/mathematics/high-school/4rq3n2rvpw3y3myem7faibeqtijvivuq5g.png)
Since DB = AC, DB + AC will be:
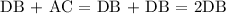
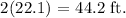
Therefore, DB + AC = 44.2 ft.
The answer is Choice B.