Question

A car was valued at $29,000 in the year 1993. The value depreciated to $15,000 by the year 2006. Assume that the car value continues to drop by the same percentage. What will the value be in the year 2009 ?What was the annual rate of change between 1993 and 2006?What is the correct answer to part A written in percentage form?

Answer 1

Given:

Original Value - $29,000

Final Value after 13 years - $15,000

Find: annual rate of change between 1993 and 2006 (13 years)

Solution:

To determine the annual rate of change, we use the formula below:

`y=ab^x`

where a = the initial value, b = the rate of change, x = the number of years, and y = the final value at x year.

Since we already have the values of the variables provided in the question, let's replace them.

`15,000=29,000(b)^(13)`

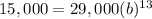
Then, solve for b.

Divide both sides of the equation by 29,000.

`(15,000)/(29,000)=(29,000b^(13))/(29,000)\Rightarrow(15)/(29)=b^(13)`

Power both sides of the equation by 1/13.

`((15)/(29))^{(1)/(13)}=(b^(13))^{(1)/(13)}\Rightarrow0.95055`

The value of b is 0.95055.

Let's subtract this from 1.

`1-0.95055=0.04945`

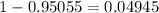
Multiply this by 100.

`0.04945*100=4.945\approx4.95\%`

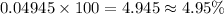
Therefore, the annual rate of change between 1993 to 2006 is -4.95%. We used negative because we are dealing with depreciation. The depreciation rate annually is 4.95%.

If the value of the car continues to drop after an additional 3 years (2006 - 2009) or 16 years from 1993, let's replace "x" in the equation above with 16, and let's use b = 0.95055 to solve for the value of the card in the year 2009.

`y_(2009)=29,000(0.95055)^(16)`

Type those values in a calculator and solve.

`y_(2009)\approx12,882.42`

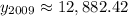
The value of the car in the year 2009 will be approximately $12, 882.42.