Question

Can you please show the steps to solve this ?

Answer 1

1) In a cyclic quadrilateral, we can tell that the opposite angles are supplementary. And, in addition to this, the sum of the interior angles is equal to:

`\begin{gathered} S_i=180(4-2) \\ S_i=180(2)\Rightarrow S_i=360 \end{gathered}`

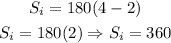
2) So now, we can write out the following equation to find x and then each angle:

`\begin{gathered} m\angle A+m\angle C=180 \\ m\angle B+m\angle D=180 \end{gathered}`

`\begin{gathered} (x+2)+(x-2)=180 \\ 2x=180 \\ x=90 \\ m\angle A=(x+2)=92 \\ m\angle B=180-80=100 \\ m\angle C=(x-2)=88 \\ m\angle D=(x-10)=80 \\ 92+100+88+80=360 \\ 360=360 \end{gathered}`

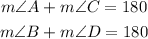
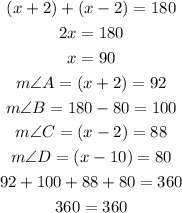
Note that we could test and verify that.