1 Answer

Laraconda · Answer 1 · 2023-09-13T10:27:30+0000

Use the next formula to write a geometric sequence as a exponential function:

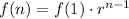
$f(n)=f(1)\cdot r^(n-1)$

f(1) is the first term

r is the common ratio

1. Find the common ratio: Divide each term into the previous term

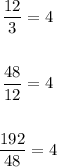
$\begin{gathered} (12)/(3)=4 \\ \\ (48)/(12)=4 \\ \\ (192)/(48)=4 \end{gathered}$

Common ratio: 4

2. Use the first term (3) and the common ratio (4) in the formula above:

$f(n)=3\cdot4^(n-1)$

Then, the given sequece written in form of a exponential function is:

$f(n)=3\cdot4^(n-1)$