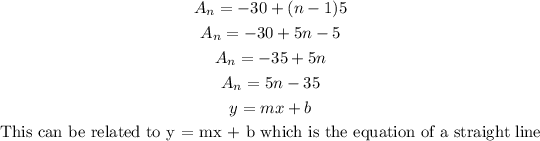Question

#1. An arithmetic sequence has a 10th term of 15 and a 14th term of 35. a.what’s the common differenceb.what is the value of the first term? use the value of D in one of the sequences equations from A.c. what is the general sequence equation for this situation?d. create a graph for this situation.e. show that the equation (y=mx+b) of this graph equals An=-30+(n-1)5.THANK YOU. i really need to pass the 9th grade ! if you could help me in less than 25 minutes that would be great since it’s timed for 25 minutes.

Answer 1

Part A

This is a question on Arithmetic Progression (A.P)

The nth term of an A.P is given as;

`\begin{gathered} A_n=a+(n-1)d \\ \text{where A}_n\text{ is the nth term} \\ n\text{ is the number of terms in the sequence} \\ d=\text{common difference} \end{gathered}`
`\begin{gathered} when=10,A_(10)=15 \\ A_(10)=a+(10-1)d \\ 15=\text{ a+9d} \end{gathered}`
`\begin{gathered} \text{when n = 14, A}_(14)=35 \\ A_(14)=a+(14-1)d \\ 35=a+13d \end{gathered}`

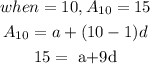
Hence, we have two linear equations to be solved simultaneously

a + 9d = 15........................ equation 1

a + 13d = 35 ..................... equation 2

Subtracting equation 1 from equation 2, we have;

13d - 9d = 35 - 15

4d = 20

`\begin{gathered} d=(20)/(4)=5 \\ d=5 \end{gathered}`

The common difference is 5

Part B

Substituting d = 5 into equation 1, we have;

a + 9(5) = 15

a + 45 = 15

a = 15 - 45

a = -30

The first term is -30

Part C

The general equation from the equation of the nth term of an A.P putting the values of a and d gotten will be;

`\begin{gathered} A_n=-30+(n-1)5 \\ A_n=-30_{}+5n-5 \\ A_n=-35+5n \end{gathered}`

Part D

From the general equation of the sequence gotten above, we can deduce that

`A_n=5n-35`

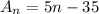
Which is similar to equation of a straight line in the form y = mx + C.

The graph to be plotted will be of the form y = 5x - 35

Part E

`\begin{gathered} A_n=-30+(n-1)5 \\ A_n=-30+5n-5 \\ A_n=-35+5n \\ A_n=5n-35 \\ y=mx+b \\ \text{This can be related to y = mx + b which is the equation of a straight line} \end{gathered}`