Let's test each scenario.
Scenario IWe are given both equations. We know that in this case, x is equivalent 0, 1, or 2 since it must be less than 3 hours. Let's test each possibility.
x = 0

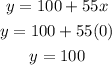
x = 1


With this information, we can immediately assume that no matter what, the first equation will always yield a larger sum than the second equation. In that case, Mechanic A is not favorable until Mechanic B's price equals that of Mechanic A.
We can visualize the graph to see that at 3 hours, however, the mechanic's will both charge the same price:
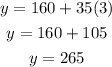
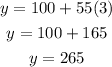
Solution
• Mechanic A is always more expensive ,until it reaches 3 hours,. Therefore, answer choice A cannot be considered since the lower repair cost would come from Mechanic B.
,
• If the repair requires less than 3 hours, Mechanic B is always favored as a cheaper price. Therefore, this choice, ,Choice B,, is correct.
,
• When 3 hours of repair are required, we cannot consider Choice C because the