Answer:
No Solution: Top- left, Top, Right
One Solution: Top - middle, Bottom -Middle, Bottom - right.
Infinitely Many solutions: Bottom- left,
Explanation:
If an equation has one solution, then the left-hand side of the equation does not equal the right-hand side.
If an equation has no solution then the slopes are the same for right and left equations; however, the intercepts are not the same. For example 3x -3 = 3x -5 has no solutions.
If an equation has infinitely many solutions, then the equation on the right is equal to the equation on the left. For example, 4x +5 = 2x + 2x + 5 which implies to 4x + 5 = 4x + 5 and therefore, it has infinitely many solutions.
With this knowledge in mind, we simplify each of the equations given.
For example, for the equation on the Top- left
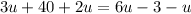
Simplifying both sides (adding like terms ) gives

The expressions on both sides of the equality sign have the same slopes but different y-intercepts; therefore, this equation has no solutions - when graphed lines 5u + 40 and 5u - 3 will never intersect.
The same goes for other equations, and in simplifying them we get the answers:
No Solution: Top- left, Top, Right
One Solution: Top - middle, Bottom -Middle, Bottom - Right.
Infinitely Many solutions: Bottom- left,