Question

A family has two cars. During one particular week, the first car consumed 20gallons of gas and the second consumed 15 gallons of gas. The two cars drove a combined total of 1025miles, and the sum of their fuel efficiencies was 60 miles per gallon. What were the fuel efficiencies of each of the cars that week?First Car: ~ miles per gallon

Second Car: ~ miles per gallon

Answer 1

If we call the efficiency of the first car as x and the efficiency of the second car as y, from the sentence "the sum of their fuel efficiencies was 60 miles per gallon.", we have the following equation

`x+y=60`

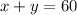
The distance travelled by a car is given by the product between the efficiency and the amount of gas consumed, therefore, the combined distance travelled is given by the sum of the products between the efficiency and the respective amount of gas consumed. The first car consumed 20 gallons of gas and the second consumed 15 gallons of gas, this means we have the following equation

`20x+15y=1025`

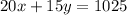
Now, we have a system with two variables and two equations

`\begin{cases}x+y=60 \\ 20x+15y=1025\end{cases}`

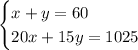
If we multiply the first one by 15 on both sides, we're going to have

`\begin{cases}15x+15y=900 \\ 20x+15y=1025\end{cases}`

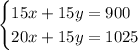
If we subtract the first equation from the second, we get a new equation only for x

`\begin{gathered} 20x+15y-(15x+15y)=1025-(900) \\ 5x=125 \\ x=(125)/(5) \\ x=25 \end{gathered}`

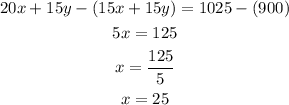
The efficiency of the first car is 25 miles per gallon.

Using our x-value on any of the previous equations give to us the y-value

`\begin{cases}x+y=60 \\ x=25\end{cases}\Rightarrow25+y=60\Rightarrow y=35`

The efficiency of the second car is 35 miles per gallon.