Solution:
Given:
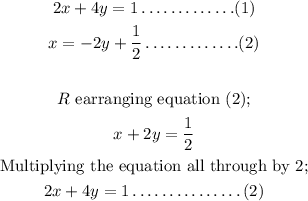
Since both equations are mathematically the same, then the graph of both linear equations are shown below;
From the above graph given, the system of two linear equations has an infinite number of solutions.
The correct answer is option B.