Question

The students at Camden Middle School went on a class ski trip. Each student paid $135 and theschool paid a total of $500. Altogether, the trip cost at most $3,335. How many students went onthe trip? Write an inequality. *

Answer 1

• Inequality: 135n+500≤3335

,

• n≤21

Explanation:

Let the number of students that went on the trip = n

Each student paid $135.

• Therefore, the amount paid by n students = $135n

,

• The school paid a total of $500

`\text{Total}=135n+500`

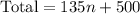
The trip cost at most $3,335, which means it costs either:

• Exactly $3,335; or

,

• Less than $3,335

We then have the inequality:

`135n+500\le3335`

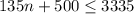
We then solve the inequality for n to find out how many students went on the trip.

`\begin{gathered} 135n+500\le3335 \\ \text{Subtract 500 from both sides} \\ 135n+500-500\le3335-500 \\ 135n\le2835 \\ \text{Divide both sides by 135} \\ (135n)/(135)\le(2835)/(135) \\ n\le21 \end{gathered}`

At most 21 students went on the trip.