Answer:
(0, -5) and (2, -8.75)
Explanations
Given the function expressed as:
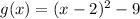
We are to find two other coordinates other than the vertex and x-intercept. Note that the equation of a parabola in vertex form is expressed as:
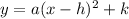
Another coordinate point is the y-intercept of the graph. The y-intercept occurs at the point where x = 0.
Substitute x = 0 into the given function;
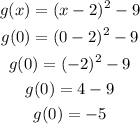
Hence the y-intercept of the graph is (0, -5)
The other coordinate of the function we can determine is the FOCUS.
The coordinates for the focus of the parabola is given as (h, k+1/4a).
where:
• a is the intercept
,
• (h, k) is the vertex
Comparing the given function with the general function, we can see that:
a = 1
h = 2
k = -9
Substitute these values into the coordinate of the focus will give:

Therefore the other two points on the graph are (0, -5) and (2, -8.75)