Question

A tennis player hits the ball with an initial speed of 62 feet per second at an angle of 15°, from a height of 2.2 feet. How far away does the ball land in feet?

Answer 1

Given:

The initial speed of teh ball =62 feet per second.

The angle is 15 degrees.

The height is 2.2 feet.

Required:

We need to find the distance from the start point to the end that is the ball land on the ground.

Step-by-step explanation:

`v_0=62,\theta=15\degree,h=2.2`

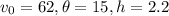
We need to find the horizontal position.

Consider the horizontal position equation.

`x=(v_0cos\theta)t`

`Substitute\text{ }v_0=62,\text{ and}\theta=15\degree\text{ in the equation}`

`x=(62cos15\degree)t`

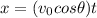
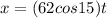
We need to find the time traveled by the ball in the air to find the distance.

Consider the vertical position equation.

`y=h+(v_0sin\theta)t-16t^2`

`Substitute\text{ }v_0=62,\text{ }h=2.2,\text{ and}\theta=15\degree\text{ in the equation}`

`y=2.2+(62sin15\degree)t-16t^2`

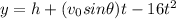
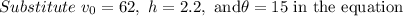
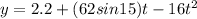
Set y =0 and solve for t.

`0=2.2+(62sin15\degree)t-16t^2`

`0=2.2+16.0468t-16t^2`

`-16t^2+16.0468t+2.2=0`

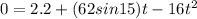
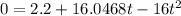
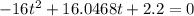
Use quadratic formula.

`t=(-16.0468\pm√((16.0468)^2-4(-16)(2.2)))/(2(-16))`

`t=(-16.0468\pm19.9574)/(-32)`

`t=(-16.0468+19.9574)/(-32),(-16.0468-19.957,4)/(-32)`

`t=-0.1222,1.1251`

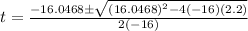
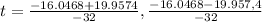
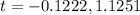
The value of time is always positive.

We get t =1.1251.

`x=(62cos15\degree)t`

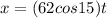
Substitute t =1.1251 in the vertical position equation.

`x=(62cos15\degree)*1.1251`

`x=67.3793feet`

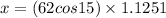
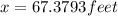
Final answer:

The ball travels approximately 67.379 feet.