Hello there. To solve this question, we have to remember some properties about linear models.
Given that she can sell up to 500 downloads for $5 each and she noticed that for each $1 increase in download price causes to 10 fewers apps are sold, we have to determine the price that will maximize her profit.
First, suppose the price is p, in the initial case we know that p = 5 but now we treat it as a variable.
Her profit will be the difference between the revenue and the expense, in this case, both are functions of p.
The revenue, denoted as R(p) is how much she can get from a dowload and this is equal to p * number of downloads.
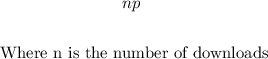
This number is an integer between 0 and 500.
If she increase the price by $1, she will sell 10 fewer apps, which means that
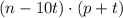
Will be the function that determines her profit considering an increase of t dollars.
Plugging n = 500 and p = 5 for the initial case, we get the equation
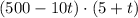
Multiply the values, such that we get
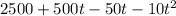
Add the similar values
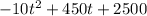
Of course, by maximizing t, we'll maximize the profit function in terms of the increase in dollars.
Since the question asks for the price, we use the following formula:

Such that we get
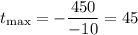
Notice that in this case she would sell each app for $50, but in the other hand 500 - 10 * 45 = 50 apps would be sold.
50 * 50 = 2500 is the maximum profit she can get by selling less apps.
Notice that 500 * 5 = 2500 as well, but she is not expected to sell everything.