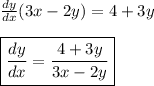Question

Find dy/dx if 3xy=4x+y^2

Answer 1

Hi there!

We can use implicit differentiation with respect to x:

`3xy = 4x + y^2`

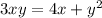
If a term with 'y' is differentiated, a 'dy/dx' must be included.

We can differentiate each term separately for the explanation.

3xy

We must use the power rule since 'x' and 'y' are both in this term.

Power rule:

`f(x) * g(x) = f'(x)g(x) + g'(x)f(x)`

`3xy \\\\f(x) = 3x\\g(x) = y \\\\f'(x)g(x) + g'(x)f(x) = 3y + 3x(dy)/(dx)`

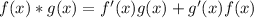
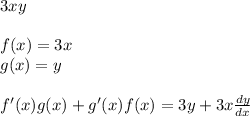
Now, we can do the others.

4x

This is a normal power rule derivative.

`f(x) = 4x\\f'(x) = 4`

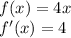
y²

Since we are not differentiating with respect to y, we must include 'dy/dx'.

`f(x) = y^2\\f'(x) = 2y(dy)/(dx)`

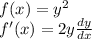
Combine the above:

`3y + 3x(dy)/(dx) = 4 + 2y(dy)/(dx)`

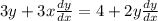
Rearrange to solve for dy/dx.

Move dy/dx to one side:

`3x(dy)/(dx) - 2y(dy)/(dx) = 4 + 3y \\\\`

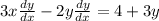
Factor out dy/dx and divide:

`(dy)/(dx)(3x- 2y) = 4 + 3y \\\\\boxed{(dy)/(dx) = (4+3y)/(3x-2y)}`