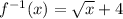Given the function:

• You can graph it.
By definition, this is the graph of the Parent Function (the simplest form) of Quadratic Functions:
The equation of this Parent Function is:
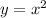
You can identify that the function given in the exercise is like the Parent Function graphed above, but translated 4 units to the right. Because, according to the Transformation Rules for Functions, when:
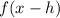
The function is shifted right "h" units.
Therefore, you can graph the function provided in the exercise:
According to the instruction given in the exercise, you have to find the domain on which the function is one-to-one and non-decreasing.
By analyzing the graph, you can determine that the function increases (goes up) on this interval:
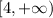
In order for that portion (the portion on the right, which is the one increasing) to be one-to-one, it has two passes the Vertical Line Test. This states that if the vertical lines intersect the graph at more than one point, it is not a One-to-One Function.
In this case, you get:
Since all the lines intersect the graph at one point, then it is a One-to-one Function.
By definition, the Domain of a function is the set of x-values for which it is defined.
Therefore, you can determine that the domain on which the function is one-to-one and non-decreasing is:
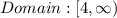
• In order to find an inverse of the function of this domain, you need to follow these steps:
1. Rewrite the function in this form:
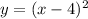
2. Solve for "x":
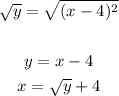
3. Swap the variables:
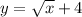
4. Rewrite it as:
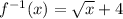
Keeping in mind the definition of Domain, you need to remember that a square root is not defined when its Radicand (the value inside the root) is negative.
Therefore, the Domains are the same:
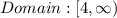
Hence, the answer is:
• Domain on which the function is one-to-one and non-decreasing:
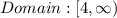
• Inverse of function on that domain: