Question

A rabbit is moving in the negative x-direction at 2.70 m/s when it spots a predator and accelerates to a velocity of 13.9 m/s along the negative y-axis, all in 2.20 s. Determine the x-component and the y-component of the rabbit's acceleration. (Enter your answers in m/s2. Indicate the direction with the signs of your answers.)

Answer 1

ax = 1.23 m/s²

ay = -6.32 m/s²

Step-by-step explanation:

The acceleration is equal to the change in velocity over time. So, the acceleration of in the x-component is equal to

`a_x=(v_(fx)-v_(ix))/(t)`

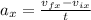
Where vfx is the final velocity on the x-direction which is equal to 0 m/s because at the end the velocity is in the y-axis. vix is the initial velocity which is -2.70 m/s and t is the time, so t = 2.20s.

Replacing the values, we get:

`a_x=\frac{0-(-2.70\text{ m/s\rparen}}{2.20\text{ s}}=1.23\text{ m/s}^2`

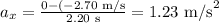
In the same way, we can calculate the y-component of the acceleration as

`a_y=(v_(fy)-v_(iy))/(t)`

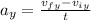
Replacing vfy = -13.9 m/s and viy = 0 m/s, we get:

`a_y=\frac{-13.9\text{ m/s - 0 m/s}}{2.20\text{ s}}=-6.32\text{ m/s}^2`

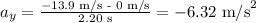
Therefore, the answer is

ax = 1.23 m/s²

ay = -6.32 m/s²