Question

An electric current heats a 250 gram sample of copper wire from 20°C to 45°C. How much heat was generated by the electric current? The specific heat capacity of copper is 0.093 cal/g•°C.

Answer 1

Given:

The mass of the copper sample is,

`m=250\text{ g}`

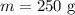
The initial temperature is,

`t_i=20\text{ }\degree C`

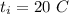
The final temperature is

`t_f=45\text{ }\degree C`

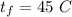
The specific heat capacity of copper is,

`c=0.093\text{ cal/g.}\degree C`

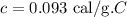
To find:

The heat generated by the electric current

Step-by-step explanation:

The heat generated by an electric current is,

`H=mc\Delta t`

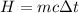
Here, the temperature difference is,

`\begin{gathered} \Delta t=45-20 \\ =25\text{ }\degree C \end{gathered}`

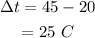
Substituting the values we get,

`\begin{gathered} H=250*0.093*25 \\ =581.25\text{ cal} \end{gathered}`

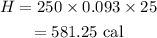
Hence, the required amount of heat is 581.25 cal.