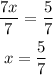1 Answer

Adamup · Answer 1 · 2023-10-12T04:54:38+0000

To solve the equation for x first, apply the distributive property to the left side:

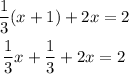
$\begin{gathered} (1)/(3)(x+1)+2x=2 \\ (1)/(3)x+(1)/(3)+2x=2 \end{gathered}$

Now add similar terms on the left side of the equation

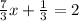
Subtract 1/3 from both sides of the equation

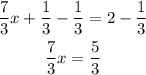
$\begin{gathered} (7)/(3)x+(1)/(3)-(1)/(3)=2-(1)/(3) \\ (7)/(3)x=(5)/(3) \end{gathered}$

Multiply by 3 on both sides of the equation

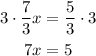
$\begin{gathered} 3\cdot(7)/(3)x=(5)/(3)\cdot3 \\ 7x=5 \end{gathered}$

Finally, divide by 7 into both sides of the equation

$\begin{gathered} (7x)/(7)=(5)/(7) \\ x=(5)/(7) \end{gathered}$

Please log in or register to add a comment.