Question

Answer the following questions:(1.1) (1.2) (1.3) (1.4) Please make sure you use a Method, do not just set parts of the function greater than or less than 0 to find answers

Answer 1

1.1) When we have an inequality and we multiply both sides by a negative number, the sign becomes its opposite.

That is, if we have a > b, when multiplying by a negative number like -1, we obtain -a < -b.

1.2) When we multiply by a positive number, the sign stays the same without changes.

1.3) We have to make two cases because for rational inequalities, we will have two intervals for the solution. In the case we multiply by (x+1) and solve as usual, we only will get one of those two intervals.

1.4) We have to solve the inequality. First we rearrange so one of the sides has the rational expression and the other side is equal to 0:

`\begin{gathered} (x-5)/(x+1)\ge2 \\ (x-5)/(x+1)-2\ge0 \\ (x-5-2(x+1))/(x+1)\ge0 \\ (x-5-2x-2)/(x+1)\ge0 \\ (-x-7)/(x+1)\ge0 \\ (x+7)/(x+1)\le0 \end{gathered}`

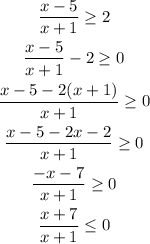
Now we can see why we would have two intervals: for the rational expression to be negative, we can have a positive numerator and a negative denominator or a negative numerator and a positive denominator.

We will now calculate the zeros of denominator and numerator.

The denominator has a zero at x = -1 and the numerator has a zero at x = -7.

This zeros will limit the solution region.

We test for a value in each of the intervals to check it the inequality stands or not.

We test for x = -10:

`\begin{gathered} (-10+7)/(-10+1)\le0 \\ (-3)/(-9)\le0 \\ (1)/(3)\le0\longrightarrow\text{False} \end{gathered}`

Now, we test with a value of x between -7 and -1, like -2:

`\begin{gathered} (-2+7)/(-2+1)\le0 \\ (5)/(-1)\le0 \\ -5\le0\longrightarrow\text{True} \end{gathered}`

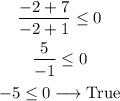
For x = -7 the rational expression is equal to 0. Because of the equal sign in the inequality, this value is included as a solution.

Finally we test for a value greater than x = -1, like x = 0:

`\begin{gathered} (0+7)/(0+1)\le0 \\ 7\le0\longrightarrow\text{False} \end{gathered}`

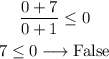
Then, the solution interval is x ∈ [-7, -1).

x = -1 is not included in the solution because it makes the rational expression undefined.

We can check with a graph: