Question

A factory that manufactures screws is performing a quality control experiment. Each object should have a length of no more than 12 centimeters. The factory believes that the length of the screws exceeds this value and measures the length of 72 screws. The sample mean screw length was 12.06 centimeters. The population standard deviation is known to be σ=0.19 centimeters.What is the null hypothesis?What is the alternative hypothesis?

Answer 1

We have a sample that will be used to test an hypothesis for the mean.

The null hypothesis is the fact that the length of the screws is not greater than 12. This can be represented as the base case, where the screws have a length that satisfy the quality requirements.

It can be represented with an equal sign, although it also includes the condition where the population length is shorter than 12 cm.

The alternative hypothesis represents the claim that we have to prove: that the population length is in fact significantly longer than 12 cm.

Then, the test tries to prove that there is significant statistical evidence (the information from the sample) to prove that the length is greater than 12 cm. In other words, prove that the null hypothesis is not true.

If we can not prove this claim, then we can not reject the null hypothesis (NOTE: this does not mean that the null hypothesis is true, but that we don't have evidence to conclude that it is false).

Answer:

Null hypothesis: H0: μ = 12

Alternative hypothesis: Ha: μ > 12

HYPOTHESIS TEST:

We have to perform the hypothesis test.

This is a right tailed test, as we want to know if the sample result is significantly higher.

The significance level is 0.05.

We have the hypothesis already written:

Null hypothesis: H0: μ = 12

Alternative hypothesis: Ha: μ > 12

Now, we analyze the sample.

We have a sample mean M = 12.06 and a sample size n = 72.

As we know the population standard deviation, we can use the z-test (NOTE: in the case we have to use the sample standard deviation, we should perform a t-test).

The population standard deviation is σ = 0.19 cm.

We continue with the calculation of the standard error:

`\sigma_M=(\sigma)/(√(n))=(0.19)/(√(72))\approx0.022`

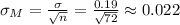
We then calculate the test statistic z as:

`\begin{gathered} z=(M-\mu)/(\sigma_M) \\ z=(12.06-12)/(0.022)=(0.06)/(0.022)\approx2.68 \end{gathered}`

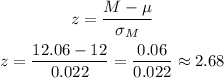
NOTE: This test statistic shows how far is the sample result from the mean, normalized to a standard normal distribution. This result shows that the sample mean is 2.68 standards error above the mean.

We can then calculate the P-value as:

`P(z>2.68)=0.00368`

This P-value (0.00368) is smaller than the significance level (0.05), which means that we have enough statistical evidence to reject the null hypothesis.

The sample shows that is very unlikely (it has a probability of 0.00368 or 0.368%) of obtaining this sample given that the length of the screws was 12 cm.