Given:
Given that the function is
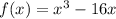
The interval is [-1,1].
Required:
To determine the mean value theorem for the given function.
Step-by-step explanation:
Since the function is continuous on [-1,1], the theorem does apply.
So, by the Mean Value Theorem for integrals, there is a number, c, in the interval (-1,1) such that
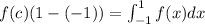
![\begin{gathered} 2f(c)=\int_(-1)^1(x^3-16x)dx \\ \\ 2f(c)=[(1)/(4)x^4-(16x^2)/(2)]_(-1)^1 \\ \\ 2f(c)=[(1)/(4)-(1)/(4)]-[8-8] \\ \\ 2f(c)=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dwvx3249hdmdygg8xwlgkhkeyac0o888jy.png)
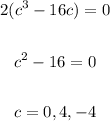
The only value of c that is in the interval (-1,1) is
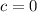
Final Answer:
The mean value theorem is applies the given function.