Question

class in which the final course grade depends entirely on the average of four equally weighted 100 points tests ,Cindy 90,78,92 on the first three .What range of scores on the fourth test Cindy will get a B for the semester (an average between 80 and 89 inclusive)? All test scores have a non negative value.put answer in interval notation

Answer 1

Notice that the final grade is the AVERAGE of the 4 tests (of 100 points each). The question is what score does she need in her fourth test in order to get a B for the class. We call this UNKNOWN score "X". Then we can perform the average as shown below:

`\begin{gathered} (90+78+92+X)/(4)=80 \\ \text{and} \\ (90+78+92+X)/(4)=89 \end{gathered}`

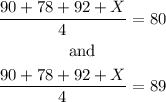
and solve for X in each equation.

Then the minimum value of X to get a "B"(average of exactly 80, can be found by multiplying both sides of the first equation by 4, and then solving for X as shown below:

90 + 78 + 92 + X = 80 * 4

260 + X = 320

subtract 260 from both sides to isolate X

X = 320 - 260

X = 60.

Now we do something similar for the maximum B score (89) expressed in the second equation we created:

90 + 78 + 92 + X = 89 * 4 = 356

260 + X = 356

subtract 260 from both sides to isolate X:

X = 356 - 260

X = 96

Therefore her scores in the last test can be between 60 and 96, which in interval notation is written as:

[60, 96] where we used square brackets because the endpoints of the interval are to be included.