Given that the vector a expressed is expressed in magnitude and direction as
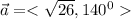
We can find the compnent form below.
Step-by-step explanation
The above form of vector a corresponds with the polar coordinates

Therefore, to get the component form we must convert to its cartesian coordinates.
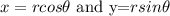
Therefore;
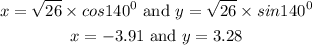
Answer: (-3.91, 3.28)