Start by sketching the rectangle
write the area as an equation
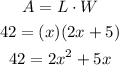
write the expression in the form of a quadratic expression
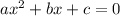
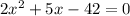
solve the equation using the quadratic equation
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
x=-6; x=3.5
since we are talking about meassurements it cannot be a negative, so the solution must be 3.5
Dimensions of the rectangles
Lenght: (2x+5) = 12
Width: 3.5