Given the system of equations:
ax + by = -12
7x + 8y = 6
Let's determine the values of a and b that make the system dependent.
Since both equations are dependent, we have:
ax + by = -12
7x + 8y = 6
Apply the formula:`

Where:
a1 = a
b1 = b
c1 = -12
a2 = 7
b2 = 8
c2 = 6
Thus, we have:
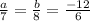
Thus, for a, consider:
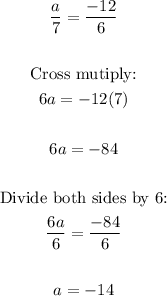
For the value of b, we have:

Therefore, the values of a and b that make the system dependent are:
a = -14
b = -16
ANSWER:
a = -14, b = -16