If the factors of a polyomials are
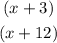
This means that the polynomial can be written as a power of thouse factors, like:
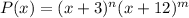
As we can see, if either of the factors zeros out, the hole polynomial you be zero too, because anything will be multiplied by zero.
So, to find the values of x that will make this polynomial equal to zero, we just solve the equation of each factor equal to zero.
So, the first possible x value is:

And the second possible value of x is:
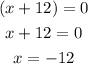
Thus, the possible values of x that make the polynomial zero are -3 and -12, which corresponds to alternative C.