Question

Please help me determine if these sequence are arithmetic geometric or neither

Answer 1

Given:

`\begin{gathered} a(1)=5,a(n)=a(n-1)+3\text{ }for\text{ }n\ge2 \\ b(1)=1,b(n)=3.b(n-1)for\text{ }n\ge2 \\ c(1)=3,c(n)=-c(n-1)+1\text{ }for\text{ }n\ge2 \\ d(1)=5,d(n)=d(n-1)+n\text{ for n}\ge2 \end{gathered}`

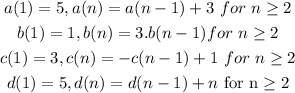
Required:

Find whether the series is arithmetic or geometric.

Step-by-step explanation:

(1) The given terms are

`5,8,11,14,17`

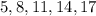
Find the common difference of the following terms.

`\begin{gathered} 8-5=3 \\ 11-8=3 \\ 14-11=3 \\ 17-14=3 \end{gathered}`

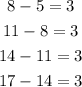
The common difference is the same between each term so the given sequence is arithmetic.

(2)The given terms are

`1,3,6,9,12,15`

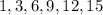
Find the common difference as:

`\begin{gathered} 3-1=2 \\ 6-3=3 \\ 9-6=3 \end{gathered}`

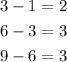
Since the common difference is not the same between each term so the given sequence is not arithmetic.

Now find the common ratio as:

`\begin{gathered} (3)/(1)=3 \\ (6)/(3)=2 \\ (9)/(6)=(3)/(2) \end{gathered}`

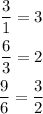
Since the common ratio is not the same between each term so the given sequence is not geometric.

Thus the given sequence is neither arithmetic nor geometric.

(3)The given terms are

`3,-2,-5,-8,-11`

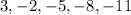
Find the common difference as:

`\begin{gathered} -2-3=-5 \\ -5-(-2)=-5+2=-3 \\ -8-(-5)=-8+5=-3 \end{gathered}`

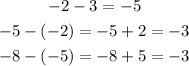
Since the common difference is not the same between each term so the given sequence is not arithmetic.

Now find the common ratio as:

`\begin{gathered} (-2)/(3)=-(2)/(3) \\ (-5)/(-2)=2.5 \end{gathered}`

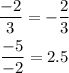
Since the common ratio is not the same between each term so the given sequence is not geometric.

Thus the given sequence is neither arithmetic nor geometric.

(4) The given sequence is:

`d(1)=5,d(n)=d(n-1)+n\text{ for n}\geqslant2`
`\begin{gathered} d(2)=d(2-1)+2 \\ =d(1)+2 \\ =5+2 \\ =7 \end{gathered}`
`\begin{gathered} d(3)=d(3-1)+3 \\ =d(2)+3 \\ =7+3 \\ =10 \end{gathered}`
`\begin{gathered} d(4)=d(4-1)+4 \\ =d(3)+4 \\ =10+4 \\ =14 \end{gathered}`
`\begin{gathered} d(5)=d(5-1)+5 \\ =d(4)+5 \\ =14+5 \\ =19 \end{gathered}`

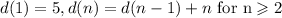
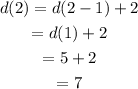
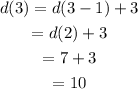
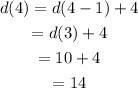
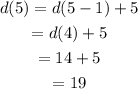
Thus the terms of the sequence are 5,7,10,14,19.