Since we want to know how much wrapping paper he used in square centimeters, we want to figure the total surface area of the gift box.
Since it is a square pyramid, the triangles of the sides are all congruent, and the base is a square.
So, tha area of the square base is the multiplication of its sides, which are equal:
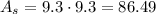
For the triangles, we can clauclate the area of one of them and multiply by 4 to get the area of all. The area of a triangle is its base multiplyed by its height divided by 2. The height is given and the base is the same as the square sides. So the area of 1 triangle is:

So, the tota area is the area of the square plus 4 times the area of one triangle:
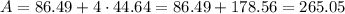
This is already in the proper unit, so the area is 265.05 cm².