Question

Find the constant variation for each direct variation where Y varies directly with X. Then find the value of y when X = 3/4Y=2 when x=6

Answer 1

A direct variation can be express as:

`y=kx`

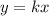
Now, we know that y=2 when x=6; plugging this values in the equation above and solving for k we have:

`\begin{gathered} 2=6k \\ k=(2)/(6) \\ k=(1)/(3) \end{gathered}`

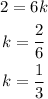
Hence our variation in this case is:

`y=(1)/(3)x`

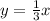
Now that we have the expression for the direct variation we plug the value x=3/4 to find y:

`\begin{gathered} y=(1)/(3)\cdot(3)/(4) \\ y=(1)/(4) \end{gathered}`

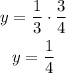
Therefore when x=3/4 the value of y is 1/4.