We have the following:
We must calculate the value of z
a.
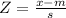
x, is the value to evalute (0.8 - 1)
m, is the mean (0.88)
s, is the standard deviation (0.3)
n, is the sample size (36)
![\begin{gathered} (0.8-0.88)/(0.3)Now,[tex]0.6554-0.3974=0.258]()
Therefore, the probability is 0.258 or 25.8%
b.
![Z=\frac{x-m}{\frac{s}{\sqrt[]{n}}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/82djefc03los0tj304hie2dg5ei764jnx3.png)
x, is the value to evalute (0.8 - 1)
m, is the mean (0.88)
s, is the standard deviation (0.3)
n, is the sample size (36)
replacing:
![\begin{gathered} \frac{0.8-0.88}{\frac{0.3}{\sqrt[]{36}}}now,[tex]0.9918-0.0548=0.937]()
Therefore, the probability is 0.937 or 93.7%