We are given the following equation:
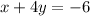
We can solve for "y" first by subtracting x to both sides:
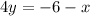
now we divide both sides by 4:

Simplifying:
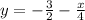
Since the equation is of the form:

This is the equation of a line. Therefore, to plot this line we only need to points. We find the points by giving values to "x".
For x = 0:
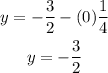
Therefore the point (0, -3/2) is part of the line.
For x = 1

therefore, the point (1, -7/4) is part of the line. Now we plot this to points and join them with a line, like this: