Question

The formula y = mx + b is the slope-intercept form of the equation of a line where m is the slope of the line, b is the y-intercept, and (x,y) is a solution of the equation. The equation solved for b is b = y - mx. True False A у – ь False The equation solved for x is x = A True The equation solved for m is m = x (y – b). True False

Answer 1

The slope-intercept form is

`y=mx+b`

If we solve for b, we have to subtract mx on each side.

`\begin{gathered} y-mx=mx-mx+b \\ b=y-mx \end{gathered}`

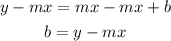
Therefore, the first statement is true.

If we solve for x, first, we subtract b on each side.

`\begin{gathered} y-b=mx+b-b \\ y-b=mx \end{gathered}`

Then, we divide the equation by m.

`\begin{gathered} (mx)/(m)=(y-b)/(m) \\ x=(y-b)/(m) \end{gathered}`

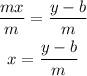
Therefore, the second statement is true.

If we solve the equation for m, first, we subtract b on each side.

`\begin{gathered} y-b=mx+b-b \\ y-b=mx \end{gathered}`

Then, we divide by x.

`\begin{gathered} (y-b)/(x)=(mx)/(x) \\ (y-b)/(x)=m \end{gathered}`

Therefore, the third statement is false.