Answer:
Step-by-step explanation:
We can notice that the triangles formed are similar to the original triangle since an altitude is drawn from the right angle.
To find the measure of x, we use ratio:
Triangle 1:
Triangle 2:
So, we use the formula:
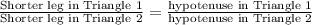
We plug in what we know:
![\begin{gathered} \frac{\text{Shorter leg in Triangle 1}}{\text{Shorter leg in Triangle 2}}=\frac{\text{hypotenuse in Triangle 1}}{\text{hypotenuse in Triangle 2}} \\ (4)/(x)=(x)/(13) \\ \text{Simplify and rearrange} \\ (x)(x)=(4)(13) \\ x^2=52 \\ x=\sqrt[]{52} \\ x=2\sqrt[]{13} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uhl609kn8vhsy27mjagwo85jp41qn9uwg1.png)
Therefore, the answer is:
![x=2\sqrt[]{13}](https://img.qammunity.org/2023/formulas/mathematics/college/46rmjjnetnwgnrjh8ap9qgz7tf3y8143w0.png)