We need to calculate the compounded function F(G(6)). To solve it we need to use the value of "G(6)" as an input for the function "F(x)". So we will first calculate G(6).
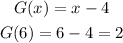
G(6) = 2. So we need to use that as an input to F(x).
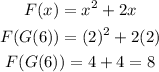
The value of F(G(6)) is 8.
Now we need to calculate the value of "G(F(-3))". This is the value of G(x) when the input is equal to F(-3). We will use the same procedure as before.

The value of F(-3) is equal to 3, so we will use that as an input to G(x).

The value of G(F(-3)) is -1.
(F o G)(0) means F(G(0)). So we need to find the value of F(x) when the input is G(0). We will do the same as before.
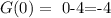
The value G(0) is equal to -4.
Now we need to use this value as an input to F(x).
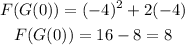
The value of (F o G)(0) is equal to 8.