Question

Solve the following system of equations by graphing. Then determine whether the system is consistent or inconsistent and whether theequations are dependent or independent. If the system is consistent, give the solution.6x + 6y = -30( 3x + 3y = -15

Answer 1

Recall that the slope-intercept form of the equations of a line is:

`y=mx+b\text{.}`

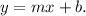
Taking both equations to their slope-intercept form we get:

`\begin{gathered} 6x+6y-6x=-30-6x, \\ 6y=-30-6x, \\ (6y)/(6)=-(30)/(6)-(6)/(6)x, \\ y=-x-5\text{.} \end{gathered}`
`\begin{gathered} 3x+3y-3x=-15-3x, \\ 3y=-15-3x, \\ (3y)/(3)=-(15)/(3)-(3)/(3)x, \\ y=-x-5. \end{gathered}`

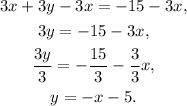
Notice that both equations are the same, therefore the system has infinitely many solutions, therefore it is consistent and dependent.

Answer:

Equations:

`\begin{gathered} y=(-1)x+(-5), \\ y=(-1)x+(-5)\text{.} \end{gathered}`

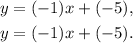
The system is consistent and dependent.

A solution to the system is (0,-5).