According to the Tangent-Secant theorem, the length of the tangent segment KL squared, must be equal to the product of the lengths of the secant segments LN and LM:
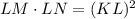
Replace KL=18, LM=12 and LN=12+(2x-9) in order to get an equation for x and find its value:
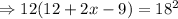
Solve for x:
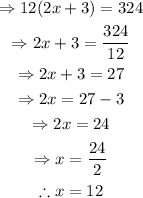
Replace x=12 in the expression for MN to find the length MN:
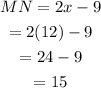
Therefore, the measure of MN is 15.
The correct choice is option C) 15.