Answer;
11.9 years
Explanations:
The formula for calculating the compound amount is expressed as:
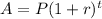
where:
• P is the ,amount invested
,
• r is the r,ate
,
• t is the ,time taken
Given the following parameters
P = $4,800
A = $12,000
r = 8% = 0.08
Substitute

Simplify to determine the value of t

Hence the time it will take for an investment of $4,800 to increase to $12,000 if it is invested at 8% per year compounded continuously is 11.9 years