Question

The kinetic friction force between a 64.0-kg object and a horizontal surface is 48.0 N. If the initial speed of the object is 25.0 m/s, and friction is the only force acting on the object, what distance will it slide before coming to a stop? Answer: _________ m/s (round to the nearest tenth)

Answer 1

First, use Newton's Second Law of Motion to find the acceleration of the object, considering that only the friction is acting on the object with a mass of 64.0kg:

`\begin{gathered} \Sigma F=ma \\ \\ \Rightarrow f=ma \\ \\ \Rightarrow a=(f)/(m)=(48.0N)/(64.0kg)=0.75(m)/(s^2) \\ \\ \therefore a=0.75(m)/(s^2) \end{gathered}`

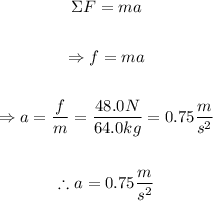
Next, remember the following formula that relates the initial and final velocities of a uniformly accelerated particle with the distance that it travels and the acceleration:

`d=(v_f^2-v_0^2)/(2a)`

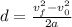
Since the object starts at 25.0 m/s and stops, then v_f=0. Since the object is decelerating, the acceleration is negative.

Replace v_0=25.0m/s, a=-0.75m/s^2 and v_f=0 to find the distance that it will slide before coming to a stop:

`\begin{gathered} d=-(v_0^2)/(2a)=-((25.0(m)/(s))^2)/(2(-0.75(m)/(s^2)))=416.666....m \\ \\ \therefore d\approx416.7m \end{gathered}`

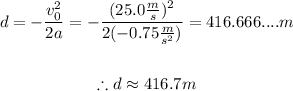
Therefore, to the nearest tenth, the distance that the object slided before coming to a stop is 416.7m.