The statements that are valid based on the graph include:
A. When the coordinates (0, 1) and (-1, 1/3) are considered, r = 1/(1/3), which simplifies to 3.
C. When the coordinates (3,27) and (2,9) are considered, r = 27/9, which simplifies to 3.
F. When the coordinates (1,3) and (2,9) are considered, r = 9/3, which simplifies to 3.
In Mathematics and Geometry, the nth term of any geometric sequence can be determined by using the following formula:

Where:
 is the nth term of any geometric sequence.
is the nth term of any geometric sequence.- r represents the common ratio.
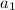 represents the first term of any geometric sequence.
represents the first term of any geometric sequence.
Based on the given statements, we would determine the common ratio as follows;
Common ratio, r =
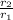
Common ratio, r = 1/(1/3)
Common ratio, r = 3.
For the coordinates (1,3) and (2,9), we have;
Common ratio, r = 9/3
Common ratio, r = 3.
For the coordinates (3,27) and (2,9), we have;
Common ratio, r = 27/9
Common ratio, r = 3.
In this context, we can logically conclude that all of the statements with a common ratio of 1/3 are not valid based on the graph.