According to the Negative exponent rule, you know that:

According to the Product of powers property, you have that:
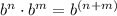
Equivalent expressions have the same value, but they are written in different forms. For this case, you have this expression:
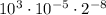
Simplify it in order to find an equivalent expression. Applying the Product of powers property:

Finally, applying the Negative exponent rule, you get this equivalent expression with only positive exponents:
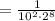
The answer is Option 2.