Question

A study determined that 4% of children under 18 years old lived with their father only. Find the probability that exactly 2 children selected at random from 12 children under18 years old lived with their father onlyThe probabilty that exactly 2 of the 12 children under 18 years old lived with their father only is?(Do not round until the final answer Thon round to the nearest thousandth as needed)

Answer 1

Binomial distribution formula:

`P(x)=_nC_x\cdot p^x\cdot q^(n-x)`

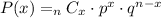
where:

P: probability

x: number of times for a specific outcome within n trials

nCx: number of combinations

p: probability of success on a single trial

q: probability of failure on a single trial

n: number of trials

We have to apply the binomial distribution for this case because a child lives or doesn't live with his/her father only.

Substituting with x = 2, p = 0.04 (=4/100), q = 0.96 (= 1 - 0.04), n = 12, we get:

`\begin{gathered} P(2)=_(12)C_2\cdot0.04^2\cdot0.96^(12-2) \\ P(2)=66\cdot0.04^2\cdot0.96^(10) \\ P(2)=0.070 \end{gathered}`

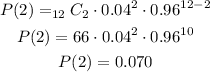
The probability that exactly 2 of the 12 children under 18 years old lived with their father only is 0.070 or 7%