Hello can I have some help for the second part of the question

Question

asked Jun 14, 2023 195k views

1 Answer

Andrew Sawa · Answer 1 · 2023-06-19T13:56:14+0000

y = - x - 2

The equation of a line perpendicular to PQ in point-slope form is given as:

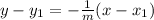
where:

• m is the ,slope, of the line

,

• (x₁, y₁) is ,any point ,on the line

Get the required point

The point (x₁, y₁) will be the midpoint of PQ with endpoints P(-5, -5) and Q(3, 3) as shown using the midpoint formula.

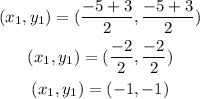
$\begin{gathered} (x_1,y_1)=((-5+3)/(2),(-5+3)/(2)) \\ (x_1,y_1)=((-2)/(2),(-2)/(2)) \\ (x_1,y_1)=(-1,-1) \end{gathered}$

Get the slope of the line passing through the point P(-5, -5) and Q(3, 3) using the slope formula as shown:

$\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(3-(-5))/(3-(-5)) \\ m=(3+5)/(3+5) \\ m=(8)/(8) \\ m=1 \end{gathered}$

Substitute the point (-1, -1) and the slope of PQ which is 1 into the point-slope form of the equation to have:

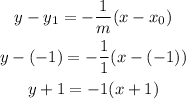
$\begin{gathered} y-y_1=-(1)/(m)(x-x_0) \\ y-(-1)=-(1)/(1)(x-(-1)) \\ y+1=-1(x+1) \end{gathered}$

Expand the parenthesis:

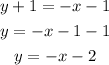
$\begin{gathered} y+1=-x-1 \\ y=-x-1-1 \\ y=-x-2 \end{gathered}$

Hence, the equation of the line passing through the midpoint and perpendicular to PQ is y = -x - 2