Question

find the solutions to the following rational equation. check for extraneous solutions. keep your answers as exact as possible.4x/x^2+x-6=7x/x^2-5x-24 +3/x^2-10x+16

Answer 1

we have the problem

`(4x)/(x^2+x-6)=(7x)/(x^2-5x-24)+(3)/(x^2-10x+16)`

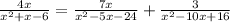
Simplify the denominators

so

x^2+x-6=(x+3)(x-2)

x^2-5x-24=(x+3)(x-8)

x^2-10x+16=(x-2)(x-8)

sustitute en la expresion original

`(4x)/(\mleft(x+3\mright)\mleft(x-2\mright))=(7x)/(\mleft(x+3\mright)\mleft(x-8\mright))+(3)/(\mleft(x-2\mright)\mleft(x-8\mright))`

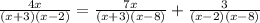
Multiplica ambos lados por (x+3)(x-8)(x-2) para eliminar fracciones

`(4x\mleft(x+3\mright)\mleft(x-8\mright)\mleft(x-2\mright))/((x+3)(x-2))=(7x\mleft(x+3\mright)\mleft(x-8\mright)\mleft(x-2\mright))/((x+3)(x-8))+(3\mleft(x+3\mright)\mleft(x-8\mright)\mleft(x-2\mright))/((x-2)(x-8))`

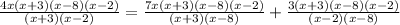
simplifica

`4x(x-8)=7x(x-2)+3(x+3)`
`4x^2-32x=7x^2-14x+3x+9`
`\begin{gathered} 4x^2-32x=7x^2-11x+9 \\ 7x^2-4x^2+32x-11x+9=0 \\ 3x^2+21x+9=0 \end{gathered}`

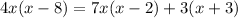
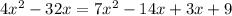
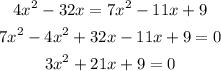
simplifica, divide por 3 toda la expression

`x^2+7x+3=0`

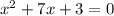
Resuelve la ecuacion quadratica utilizando la formula

a=1

b=7

c=3

sustituye

`x=\frac{-7\pm\sqrt[]{7^2-4(1)(3)}}{2(1)}`
`x=\frac{-7\pm\sqrt[]{27}}{2}`

Las soluciones son

`x=\frac{-7+\sqrt[]{27}}{2}`
`x=\frac{-7-\sqrt[]{27}}{2}`