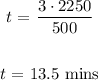We will investigate how to use ratios to determine the required quantity.
We are given the distance that Santa can fly over a period of time. We can go ahead and tabulate in the following form:
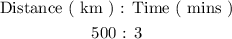
We will use the above relation to determine the time it takes ( t ) for Santa to go 2,250 kilometers. We can go ahead and update the table:

We will use the direct proportions to evaluate the value of time ( t ) required as follows:

Using the single variable equation developed above to evaluate for ( t ) as follows: