A reference angle of an angle θ is the angle that is the difference of θ to the horizontal axis.
Each angle depending on the quadrant will have different equations to find the reference angle.
We have to find angles that have the same reference angles as 117°.
The reference angle for 117° can be expressed and calculated as:
As 117° is located in the second quadrant, the reference angle is calculated as:

We can now start with the angles with the same reference angle of 63°.
First quadrant
Reference angles for angles in the first quadrant are congruent, so the answer for this quadrant is 63°.
Second quadrant
This will match the angle 117°.
Third quadrant
In this case, the reference angle will be the difference between the angle and 180°, so we can write:
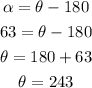
Fourth quadrant
In this case, the reference angle will be 360° minus the angle, so we can calculate it as:
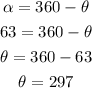
Answer:
Quadrant I: 63°
Quadrant II: 117°
Quadrant III: 243°
Quadrant IV: 297°