Question

If the initial velocity of the gasoline (p=749 kg/m?) is 5m/s, the final velocity is 10 m/s, and the initial pressure is 110 kPa, what is the value of the final pressure?

Answer 1

Given:

• Initial velocity = 5 m/s

,

• Final velocity = 10 m/s

,

• Initial pressure = 110 kPa

,

• Density = 749 kg/m³

Let's find the value of the final pressure.

Apply Bernoulli's equation:

`(P_1)/(\rho_g)+(v_1^2)/(2g)=(P_2)/(\rho_g)+(v_2^2)/(2g)`

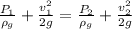
Now, simplify the equation:

`(P_1-P_2)/(\rho_g)=(v_2^2-v_1^2)/(2)`

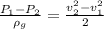
Where:

P1 is the initial pressure = 110 kPa

P2 is the final pressure

v2 is the final velocity = 10 m/s

v1 is the initial velocity = 5 m/s

ρg is the density = 749 kg/m³

Plug in values into the equation and solve for the final pressure, p2.

We have:

`\begin{gathered} (110-P_2)/(749)=(10^2-5^2)/(2) \\ \\ (110-P_2)/(749)=(100-25)/(2) \\ \\ (110-P_2)/(749)=37.5 \end{gathered}`

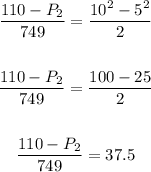
Soling further:

`\begin{gathered} 110-P_2=37.5*749 \\ \\ 110-P_2=28087.5\text{ Pa} \\ \\ 110-P_2=28.0875\text{ kPa} \\ \\ P_2=110-28.0875 \\ \\ P_2=81.9\approx82\text{ kPa} \end{gathered}`

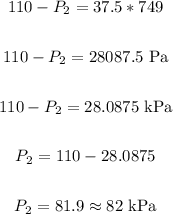
Therefore, the final pressure is 82 kPa

ANSWER:

d. 82 kPa