Given: The systems of inequalities below
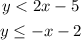
To Determine: The graphical solution of the system of inequalities
Calculate the coordinates of the x-intercept and the y-intercept of the first equation
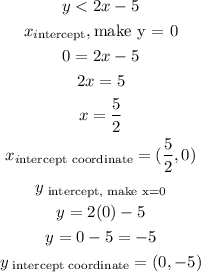
Calculate the coordinates of the x-intercept and the y-intercept of the second equation

Let us graph the solution of the system of inequalities as shown below
Hence, the solution of the system of inequalities is the area shaded purple in the above graph excluding the points at the edges of the broken line for y < 2x -5
For example (5, -5)