First, we have to find the equation of the blue and red lines.
Blue line.
Let's use the points (-3, 0) and (0, 1). We use the slope formula.

Replacing the points, we have.
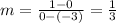
The equation of the blue line is
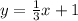
Red line.
Let's use the points (1,1) and (2,3).
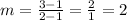
The equation of the red line is
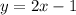
Then, we find the inequality signs for each equation. Notice that the area of the solution is above the blue line and on top of the red line.
So, the inequalities are
