Question

solve the following system of linear equation graphically 2x-3y-17=0 and 4x+y-13=0. shade the region bounded by the above lines and x-axis

Answer 1

In order to graph each equation we need to first isolate the "y" variable. This is done below:

`\begin{gathered} 2x\text{ - 3y - 17 = 0} \\ 3y\text{ = 2x - 17} \\ y\text{ = }\frac{2x\text{ - 17}}{3} \end{gathered}`
`\begin{gathered} 4x\text{ + y - 13 = 0} \\ y\text{ = -4x + 13} \end{gathered}`

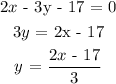
We now need to find the points where the lines cross the "y" axis and the "x" axis. The point for which the line crosses the "y" axis happens when x is equal to 0, while the point where the line crosses the "x" axis happens when y is equal to 0.

First equation:

y-axis

`y\text{ = }\frac{2\cdot0\text{ - 17}}{3}\text{ =-}(17)/(3)\text{ =-5.68 }`

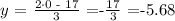
x-axis

`\begin{gathered} 0\text{ = }\frac{2\cdot y\text{ - 17}}{3} \\ 2\cdot y\text{ - 17 = 0} \\ 2\cdot y\text{ = 17} \\ y\text{ = }(17)/(2)\text{ = 8.5} \end{gathered}`

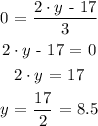
Second equation:

y-axis

`y\text{ = -4}\cdot0\text{ +13 = 13}`

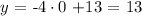
x-axis

`\begin{gathered} 0\text{ = -4}\cdot x\text{ + 13} \\ 4x\text{ =13} \\ x\text{ = }(13)/(4)\text{ = 3.25} \end{gathered}`

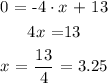
We can now draw the graphs using this informations. We need to draw a line that passes through the x-axis and y-axis of each equation.

The solution for this system of equation is the point where both lines cross. In this case (4,-3).