Question

a girl start at A and walk 2km south to B she then walk 3km west to C Find the distance and bearing of C from A

Answer 1

A girl start at A and walk 2km south to B she then walk 3km west to C.

The diagrammatic representation is shown below

To find the distance of C from A "AC", we apply the Pythagorean theorem formula which is

`\begin{gathered} (Hypotenuse)^2=(Opposite)^2+(Adjacent)^2 \\ Opposite=2\text{ km} \\ Adjacent=3\text{ km} \\ Hypotenuse=AC \end{gathered}`

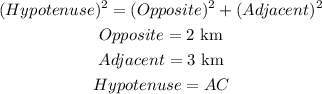
Substitute the values into the formula above

`\begin{gathered} (AC)^2=2^2+3^2=4+9=13 \\ (AC)^2=13 \\ Square\text{ root of both sides} \\ √((AC)^2)=√(13)\text{ km} \\ AC=3.61\text{ km \lparen nearest hundredth\rparen} \end{gathered}`

Hence, the distance of C from A is 3.61 km (nearest hundredth)

To find the bearing of C from A, we find the value of θ,

Applying SOHCAHTOA

`\begin{gathered} \tan\theta=(Opposite)/(Adjacent)=(2)/(3) \\ \theta=\tan^(-1)(0.6667) \\ \emptyset=33.69\degree\text{ \lparen nearest hundredth\rparen} \end{gathered}`

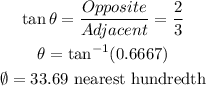
The bearing of C from A will be

`\begin{gathered} Bearing\text{ of C from A}=180\degree+(90\degree-\theta) \\ Bearing\text{ of C from A}=180\degree+90\degree-33.69\degree=236.31\degree \\ Bearing\text{ of C from A}=236.31\degree \end{gathered}`

Hence, the bearing of C from A is 236.31°